现在很多模型都采用了 MoE 架构,也有很多模型在探索稀疏 Attention,但我们会发现激活参数量、激活 Token 量和最终的性能不是那么地线性相关,甚至有时候反而性能会劣化。
探究其中的原因,其实这些稀疏化措施落实在真实的计算中,可能没那么稀疏。这里我以显存访问为例,估算稀疏化实际能减少的显存访问量。我将每次稀疏化选择(TopK)当作一次抽卡,每次抽 K 张卡,预估 N 次以后会抽到多少张不重复的卡。
你会发现,多次抽卡和一次抽卡,集卡总数有着数倍的差异,我把它叫做抽卡效应。
MoE
MoE 里要抽的卡就是专家,在每一层总共 N 个专家,每次 TopK 计算抽 K 个。在 Decode 阶段,Batch 中的每个 Deocde Token 就是一次抽卡,那在整个 Batch 计算中,被激活的总专家数,就是 B 次抽到的不重复卡数。
这个数该怎么估计呢?假设这个抽卡的概率是均匀的,也就是每个专家被激活的概率相同,随便扔给一个模型,应该就能给出下面这个公式:
总共有 N 张卡,每次抽 K 张,经过 B 次后,抽到的不重复卡的期望是多少?\( E = N \times \left[ 1 - \left( \frac{N-K}{N} \right)^B \right] \)
通过这个公式,我们就可以计算出,不同的 Batch Size 下,在一步 Decode 计算中,MoE 被激活的专家数期望(概率均值)是多少。我根据这个公式,画出下面两幅图:
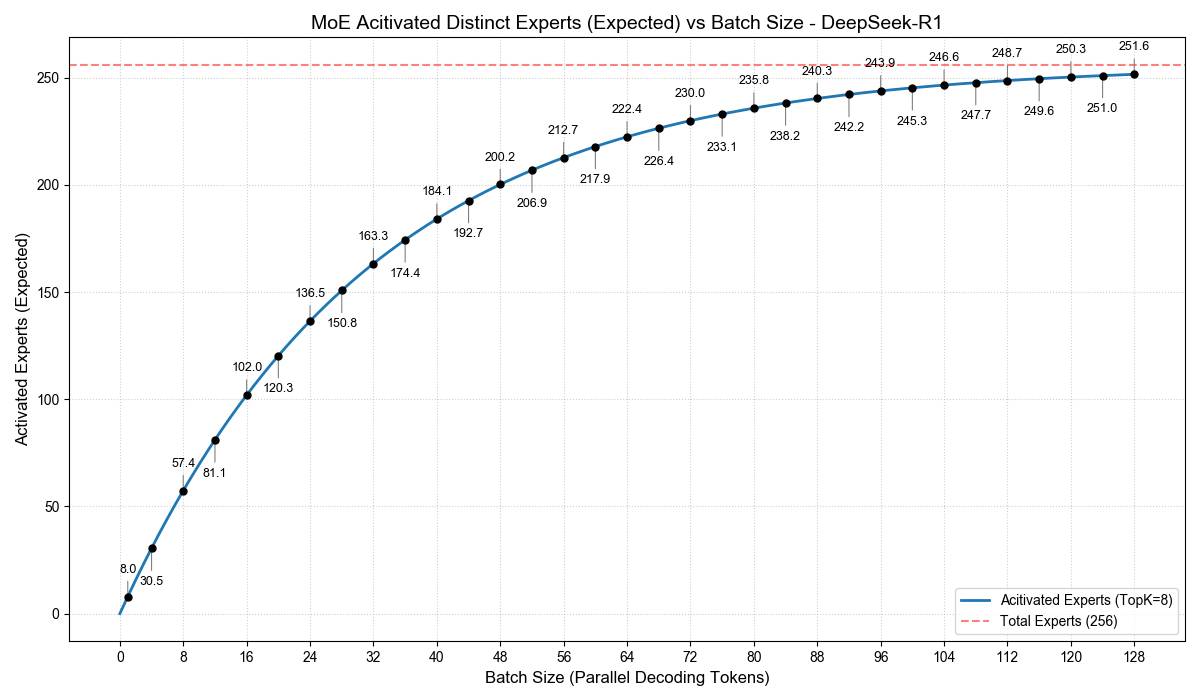
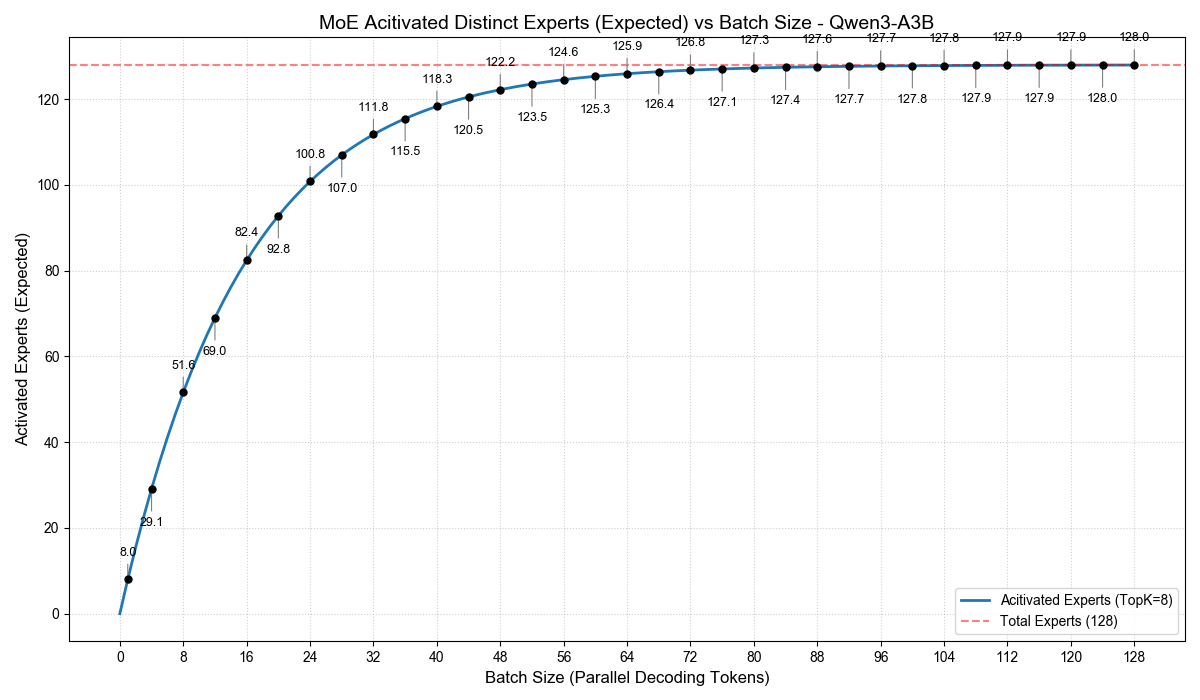
尤其是 Qwen3-A3B,我们可以看到,当 Batch Size 为 32 时,激活的专家数已经达到 111.8,相当于总专家数的 87%。也就是说,虽然每个 token 只激活了 3B,但 Batch 32 时,解码计算中激活的总参数量至少高达 26B。
只是这些参数的计算规模会小一点,但你至少要将它们从显存中读取一次。在 Decode 这种 memory bound 的计算场景下,并不是一个小的开销。
这也是我们为什么不能把 A3B 的吞吐等同于一个 Dense 3B 的吞吐。在实际追求吞吐的场景中,A3B 大概是和一个约 9B 的 Dense 模型性能相当。
在 prefill 计算中,相当于 Batch*Seqlen 次抽卡,那激活的专家数就更多了。
Sparse Attention
稀疏 Attention 里要抽的卡是 KV Cache,所以它和 Batch 无关,只和 Seqlen 有关,重复抽卡主要发生在 prefill 阶段。假设这里使用的是 DeepSeek Sparse Attention,序列长度为 N,每次通过 indexer 抽取 TopK,但是每个 Token 只能抽自己前面的 Token。被激活的总 Token 数,就是 N 次抽卡的抽到的不重复 token 数。
这个数该怎么估计呢?假设这个抽卡的概率是均匀的,还是扔给模型:
假设初始有 K 张卡,每次抽 K 张,每抽 1 次,增加 1 张卡,总共抽 N-K 次,抽到的不重复卡的期望是多少?
模型给我的都是非常简洁的答案,比如:E = N - 2 或者 E = N * K / (K+1),总之非常接近 N,我也懒得验算了。
也就是说,在 DSA 的 prefill 计算中,仍然几乎所有 Token 的 kv 都会参与到计算中,区别仍然是计算强度。但别忘了,indexer 也有自己的 kv 计算,也有自己的 kv cache。计算强度下降,访存还增加了,也许有可能导致 prefill 从 compute bound 变成 memory bound(瞎写的,没测算)。
DeepSeek V3.2 Exp 的报告里有这样一句:
Note that for short-sequence prefilling, we specially implement a masked MHA mode to simulate DSA, which can achieve higher efficiency under short-context conditions.
应该也是应对在短上下文场景下,稀疏化反而导致性能劣化严重的情况。