PFOR-DELTA 是一种经典的有序整数数列压缩算法,被广泛使用在搜索、推荐引擎的倒排索引和召回队列压缩中。PFOR-DELTA 的具体算法这里就不展开了,不了解的同学可以参考它的原始论文《Super-Scalar RAM-CPU Cache Compression》或者做一些搜索工作。
朴素的 PFOR-DELTA 解压主要是逐个对 frame 中的 bitpack 整数进行解压,对朴素 PFOR-DELTA 的优化主要包括对齐的内存访问(aligned memory access, 先按4/8字节偏移读取,然后再移位取得 bitpack)和循环展开(loop unrolling, 由每次循环解压一个整数转成每次循环解压 N 个整数以减少分支判断和访存次数)。通用的 PFOR-DELTA 函数库,往往采取这两种优化方法。
本文主要介绍在目前的先进 CPU 架构下,如何利用 SIMD 指令(如 SSE, AVX) 加速 PFOR-DELTA 解压和查找。中文互联网上与之相关的有一篇阿里搜索和推荐团队的文章《索引压缩算法New PForDelta简介以及使用SIMD技术的优化》,但该文章缺乏算法细节且其收益表明对 SIMD 指令的应用并不高效。与该文类似,为简化计,下文主要以不带异常段的 PFOR-DELTA 为例来说明算法细节。
基于 SIMD 的 bit unpacking
PFOR-DELTA 的每个分块中,都是以固定位宽压缩的整数。例如小于 32 的整数,都可以用 5 位来存储,相比于原来的 32 位存储,大大减少了数据的存储空间。但是在使用的时候,我们又必须将压缩的数展开到 32 位,才能进计算和比较操作,将一个数从压缩的位宽展开到使用的位宽,叫做 bit unpacking。
对单独一个 bitpack 的整数来说,展开是非常容易的,通过简单的移位、AND 操作即可完成。但是 SIMD 指令主要提升的是并行化,考虑到 frame 宽度不同,存在各种对齐问题,如何同时进行多个数的 bit unpacking 并不是一件非常直观的事。
下面以 frame 宽度为 9,即每个整数用 9 bit 表示,来详细说明基于现代 CPU 广泛支持的 128位 SIMD 指令的 bit unpacking 算法。256/512 位的 SIMD 算法可依此推演。
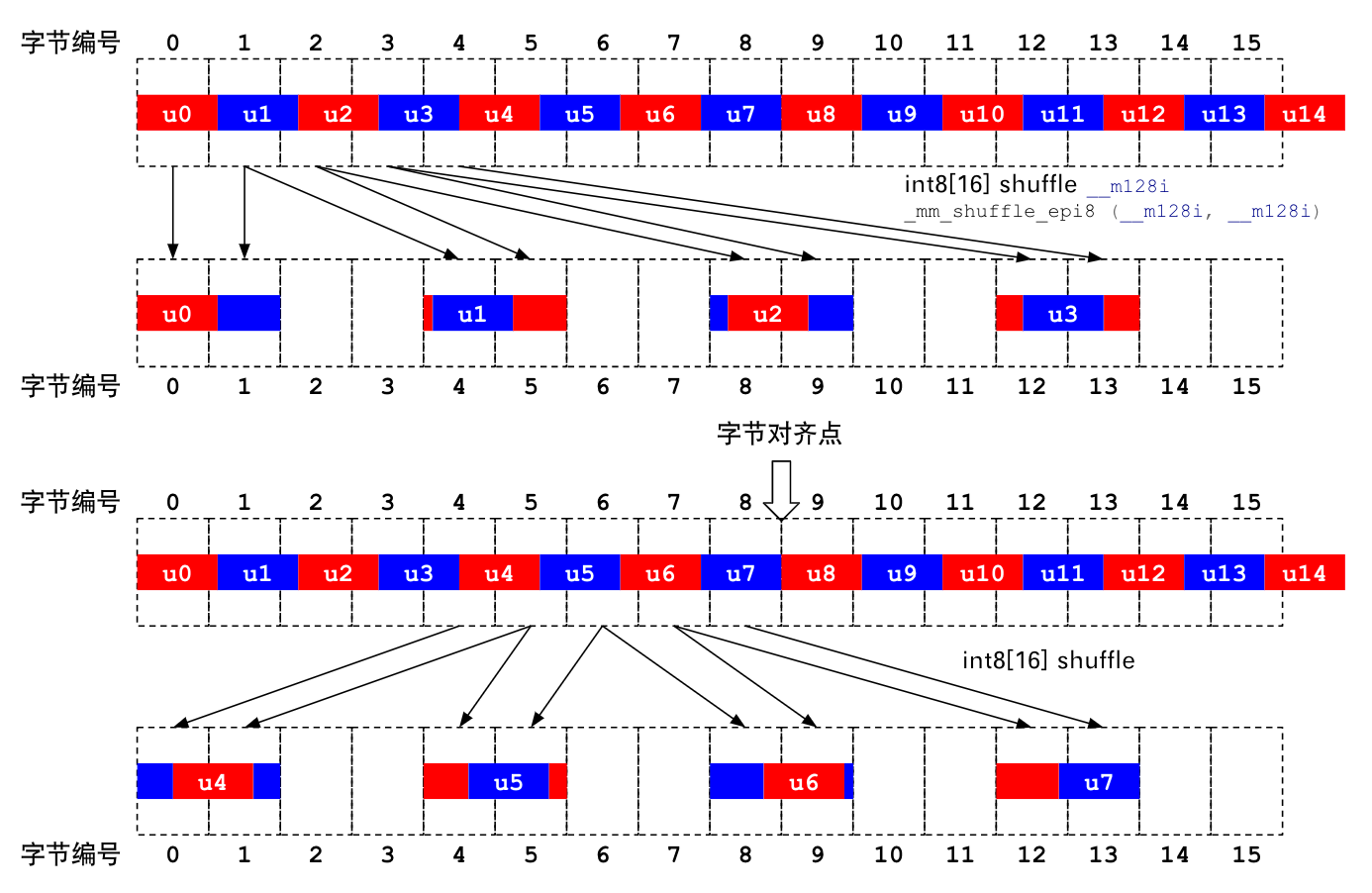
如上图所示,如果我们从数组开头加载 128 bit 的数据,其中将会包括 14 个完整的 9 bit 整数,以及多读的 2 个 bit。
为了将每个 9 bit 展开成 32 bit,在只有 128 位寄存器的情况下,我们只能 4 个 4 个地展开。首先需要将头 4 个 9 bit 整数移动到寄存器 32 位偏移的位置。Intel 提供了 _mm_shuffle_epi8 intrinsic 可以根据重整参数重新排布 128 位寄存器的内容,但可惜的是它最小粒度只能按 byte 重整,这也就意味着我们必须将 9 bit 整数所在的整个 2 byte 移动到 32 位偏移的位置。对应的代码是:
// 考虑到 litten endian,实际上 shufkey 内容为:
// 00018080 01028080 02038080 03048080
__m128i shufkey = {0x8080020180800100, 0x8080040380800302};
v = _mm_shuffle_epi8(v, shufkey);
这时候,128 位寄存器中的每个 32 位槽位中都包含一个 9 bit 整数,但可惜的是它都包含了前后数字的一些冗余 bit。下面这张图,说明了如何用 SIMD 指令消除这些冗余 bit。
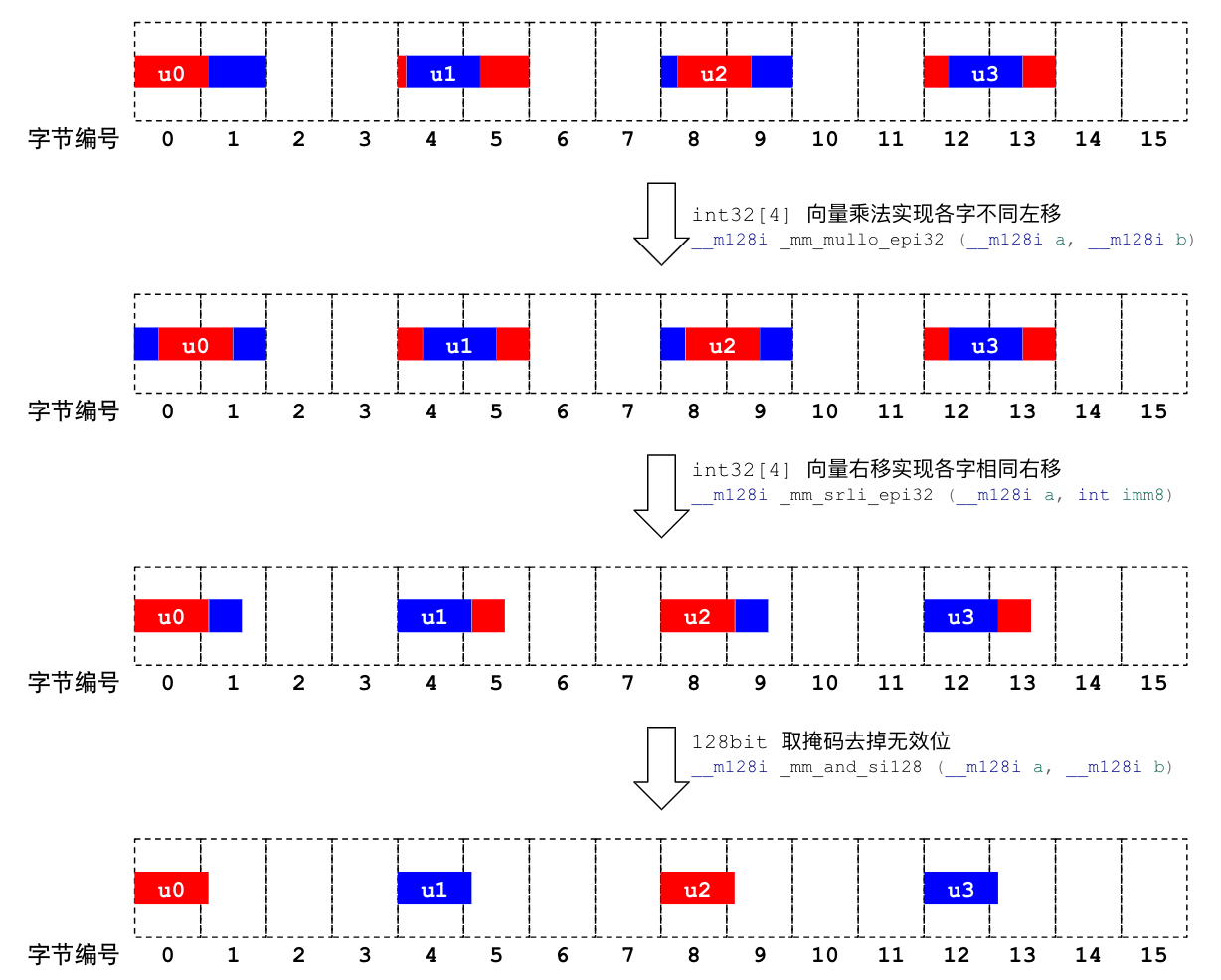
前面说过,对一个整数做 unpack 可以完全用移位和 AND mask 来实现,对多个整数依然如此。但由于各槽位中 9 bit 整数的对齐不同,移位 bit 数也不同。例如:第一个槽位右移 0 位,第二个槽位右移 2 位,第三个操作右移 2 位,第四个槽位右移 3 位。
可是 SSE 的移位指令只能支持各槽位同等位数的移位,无法支持这样各槽位不同位数的移位。我们不得不用代价更高昂的其它指令来实现分槽位不同移位,先用基于 2 次幂的向量乘法实现左移对齐 9 bit 整数,然后再统一右移,统一 mask。不使用 2 次幂除法的原因是除法的成本更高。对应到代码是:
// 通过向量乘法实现各 DW 槽位中 9 bit 整数左移对齐。当然参数可以换成常数。
v = _mm_mullo_epi32(v, _mm_set_epi32(8, 4, 2, 1));
// 所有 DW 右移 3 位
v = _mm_srli_epi32(3);
// 通过 and mask 掉 9 bit 之外多余的 bit。当然参数可以换成常数。
v = _mm_and_si128(v, _mm_set1_epi32(0x1ff));
这样,我们就实现了 9 bit 整数的 unpacking。上述算法具备通用性,对于其它的 frame 宽度,只是 shuffle、移位、乘法、mask 的参数不同,处理过程并无区别。
认真的读者可能会有疑问:第一张图为什么做了两遍 shuffle?这是考虑到了奇数位 bit packing 的特殊性。
对于偶数位(2,4,6,8)的 bit packing,一次解压 4 个整数,解压的位宽是可以被 8 整除的,所以每次解压都可以从字节边界开始,所有算法参数都相同;对于奇数位(3, 5, 7, 9),一次解压 4 个整数,解压的位宽是不能被 8 整除的,所以第二轮解压不能从字节边界开始,第二轮解压的算法参数与第一轮不同。但解压 8 个整数后,位宽就对齐到字节边界了。所以说:frame 位宽为偶数的 SIMD unpacking,循环 block 可以是 4*位宽;但 frame 位宽为奇数的 SIMD unpacking,循环 block 只能是 8*位宽。如果 AVX 指令可用,可以使用 256 位的 SIMD 指令,能大大缓解这个问题。
不失其一般性,可以看到我们只用了 4 条 SIMD 计算指令,就完成了 4 个整数的 bit unpacking,其效率较逐一 unpacking 高了很多,并且可以推及到 256 位和 512 位的情形得到更高加速比。
本节内容主要参考了论文《SIMD-Scan: Ultra Fast in-Memory Table Scan using on-Chip Vector Processing Units》。
基于 SIMD 的 delta 计算
在 PFOR-DELTA 算法中,每个整数其实是 delta,需要把所有前序的整数加起来才是真正所要的数据。参考上节,我们虽然解压出来了 {v0, v1, v2, v3},但实际上需要的却是 {v0, v0+v1, v0+v1+v2, v0+v1+v2+v3}。
将 __m128i 转成一个数组,然后再循环相加是比较简单的思路。但我们也可以直接用三条 SIMD 指令来实现 delta 计算:
// {v0, v1, v2, v3} + {0, 0, v0, v1} = {v0, v1, v0+v2, v1+v3}
v = _mm_add_epi32(_mm_slli_si128(v, 8), v);
// {v0, v1, v0+v2, v1+v3} + {0, v0, v1, v0+v2} = {v0, v0+v1, v0+v1+v2, v0+v1+v2+v3}
v = _mm_add_epi32(_mm_slli_si128(v, 4), v);
// {v0, v0+v1, v0+v1+v2, v0+v1+v2+v3} + {acc3, acc3, acc3, acc3}
acc = _mm_add_epi32(v, _mm_shuffle_epi32(acc, 0xff));
同样,不失一般性,这种错位相加的方法完全可以推广到 8 维整数向量的 delta 计算,可以推广到 256 位和 512 位的情形得到更高的加速比。
本节内容主要参考了论文《SIMD Compression and the Intersection of Sorted Integers》。
基于 SIMD 的查找比较
对 PFOR-DELTA 解压完成之后对有序数组,如果想找到某个整数的位置,我们还需要逐个进行比较。这种比较,也可以用 SIMD 指令完成:
// 初始化一次
__m128i key = _mm_set1_epi32(v_to_find);
// 向量比较
v = _mm_cmplt_epi32(key, acc);
// 比较结果处理
int res = _mm_movemask_epi8(v);
if (res != 0) {
index += __builtin_ctz(res) >> 2;
} else {
index += 4;
}
总结
综上,本文描述了完全使用 SIMD 指令进行 PFOR-DELTA 解压和查找的详细算法,给出了在 SSE 指令集下的具体代码,并且可以推广到更高的数据宽度下。至于优化的收益,将根据基线实现的不同存在差异,感兴趣的读者可以自行实现比较一下。
此外,上文的实现主要着眼通用性,针对特定的小宽度整数,其实可以使用更小的计算粒度以增大并行度。对性能有苛求的读者可自行研究。