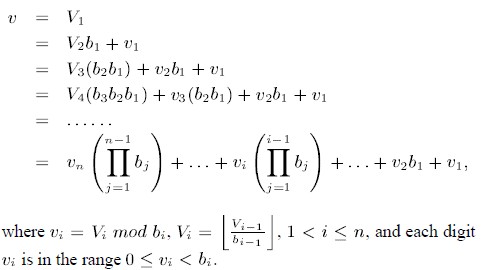摘要:bitmap 索引是一种典型的数据库索引方案,本文基于 Fastbit 软件包,使用实际用例对一些常用的 bitmap 索引算法进行了一个较为系统的介绍。
一、Fastbit是什么?
引用 Fastbit 的官方网站上的介绍:Fastbit是一个追随 NoSQL(Not Only SQL) 运动精神的开源的数据处理程序库,它提供了一系列的用压缩的 bitmap 索引支持的查询函数。在这里,我们关注的关键词是“bitmap 索引”。Fastbit 使用的是按列存储方式,其 bitmap 索引也是在按列存储的数据上建立起来的。
二、Fastbit 中的 bitmap 索引算法
Fastbit 的源代码有着非常清晰的结构。在 Fastbit 的源代码中,每个索引算法都用一个 C++ 类来实现,所有的索引算法类都是基类 index 的派生,并且在 fastbit 源代码中保存为以 i 开头的源文件。
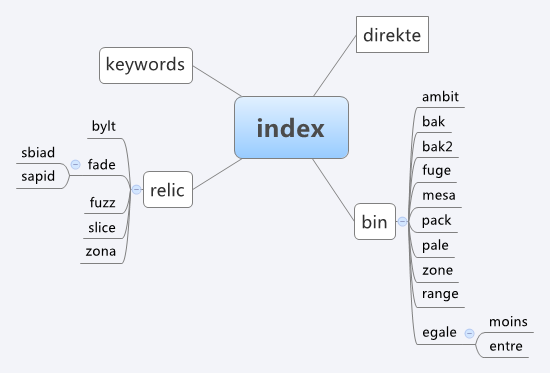
下面是 Fastbit 中的索引类的派生关系图,从美观考虑,直接使用 xmind 思维导图而不是 UML 来展现了:
下面我们将对其中部分算法进行简单的介绍。我们将这些索引算法分为几大类:基础算法、扩展算法、多层算法和多成分算法。
三、基础 bitmap 索引算法
基础的 bitmap 索引算法是最简单的 bitmap 索引算法,给出了 bitmap 索引的基本原理。
3.1 relic
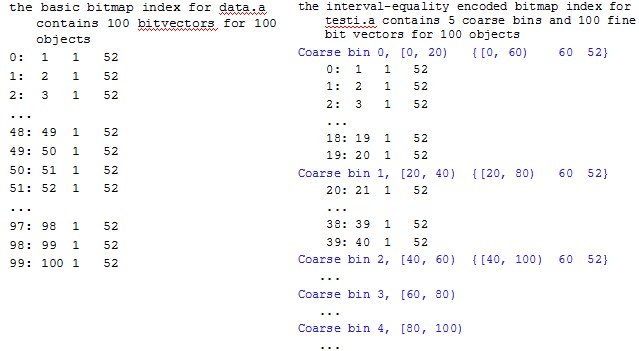
relic (定义在 irelic.h 中,实现在 irelic.cpp ) 是最原始的 equality-encoded 算法,这个单词代表“遗迹”的意思。它可谓是最简单直观的 bitmap 索引算法。relic 为需要索引的每个值都建立一个 bitvector,在该 bitvector 中,只有等于该值的列才会被置 1,其它位都被置 0,如下表所示:
| 数据 | 索引(bitmap) | ||||
| a | b | d | e | g | |
| a | 1 | 0 | 0 | 0 | 0 |
| g | 0 | 0 | 0 | 0 | 1 |
| d | 0 | 0 | 1 | 0 | 0 |
| e | 0 | 0 | 0 | 1 | 0 |
| b | 0 | 1 | 0 | 0 | 0 |
| d | 0 | 0 | 1 | 0 | 0 |
| g | 0 | 0 | 0 | 0 | 1 |
| e | 0 | 0 | 0 | 1 | 0 |
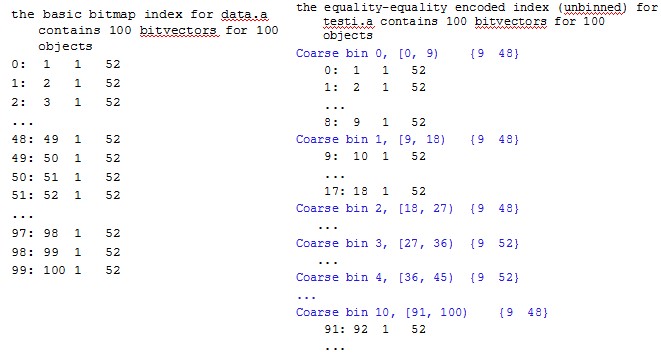
3.2 bin
bin (定义于 ibin.h,实现在 ibin.cpp)是 binned equality-encoded 算法,这里它代表“桶”的意思。它可以视为是 relic 的一种变形,它将值域分为几个不相交的区间,将原本是相等才置一的规则转变为值落在该区间内就置一,如下表所示。当然,relic 也可以视为 bin 的一个特例(将区间定义为 [a, a+ε)。bin 每个区间的范围由程序遵从某些规则设定,这些规则由命令行通过参数传入。
| 数据 | 索引(bitmap) | ||
| (…,b) | [b,e) | [e,…) | |
| a | 1 | 0 | 0 |
| g | 0 | 0 | 1 |
| d | 0 | 1 | 0 |
| e | 0 | 0 | 1 |
| b | 0 | 1 | 0 |
| d | 0 | 1 | 0 |
| g | 0 | 0 | 1 |
| e | 0 | 0 | 1 |
3.3 bin->range
range (定义于 ibin.h,实现于 irange.cpp)是 range-encoded 算法,这里它代表“范围”的意思。正如它字面所表达的意思,range 的每个 bitvector 标记着小于某边界值的值,如下表所示。因此,它可以视为是 bin 的一个累积表示,这也是 fastbit 软件包中所做的:首先构造 bin,然后累加转换成 range。值得注意的是,一般最后一列代表着小于无穷大,因此该 bitvector 全为 1,会被略去不写。
| 数据 | 索引(bitmap) | ||
| (…,b) | (…,e) | (…,g) | |
| a | 1 | 1 | 1 |
| g | 0 | 0 | 0 |
| d | 0 | 1 | 1 |
| e | 0 | 0 | 1 |
| b | 0 | 1 | 1 |
| d | 0 | 1 | 1 |
| g | 0 | 0 | 0 |
| e | 0 | 0 | 1 |
3.4 bin->mesa
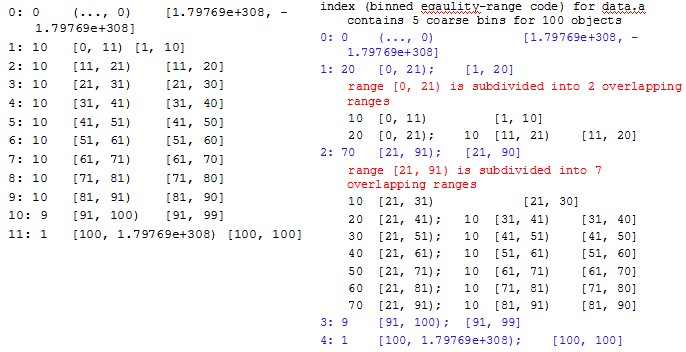
mesa (定义于 ibin.h,实现于 imesa.cpp)是 interval-encoded 算法[1],它与 bin 类似,只不过它的区间之间有重叠部分。与 range 相同,在 fastbit 软件包中,它也是通过 bin 构造起来的。
| 数据 | 索引(bitmap) | |||
| (…,d) | [a,e) | [b,g) | [d,…) | |
| a | 1 | 1 | 0 | 0 |
| g | 0 | 0 | 0 | 1 |
| d | 0 | 1 | 1 | 1 |
| e | 0 | 0 | 1 | 1 |
| b | 1 | 1 | 1 | 0 |
| d | 0 | 1 | 1 | 1 |
| g | 0 | 0 | 0 | 1 |
| e | 0 | 0 | 1 | 1 |
四、扩展 bitmap 索引算法
4.1 direkte
direkte (定义于 idirekte.h,实现于 idirekte.cpp)是丹麦语中的 direct,它与 relic 几乎是一样的,不同点只是它为小于最大值的所有值都建立了一个 bitvector(即使该值并不存在于列中)。
| 数据 | 索引(bitmap) | ||||||
| a | b | c | d | e | f | g | |
| a | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| g | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| d | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| e | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| b | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| d | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| g | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| e | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
4.2 relic->slice
slice(定义于 irelic.h,实现于 islice.cpp)实现了 O'Neil'97 [2] 提出的 bit-slice 算法。它的基本思想就是首先将原始数据用二进制进行编码,bitmap 就是所有值的二进制编码表示的集合,bitvector 的个数由最大值的二进制表示决定,如下表所示:
| 数据 | 编码 | 索引(bitmap) | ||
| a | 0 | 0 | 0 | 0 |
| g | 4 | 1 | 0 | 0 |
| d | 2 | 0 | 1 | 0 |
| e | 3 | 0 | 1 | 1 |
| b | 1 | 0 | 0 | 1 |
| d | 2 | 0 | 1 | 0 |
| g | 4 | 1 | 0 | 0 |
| e | 3 | 0 | 1 | 1 |
4.3 bin->bak
bak (定义于 ibin.h,实现于 idbak.cpp)是丹麦语中的 bin,因此它是 bin 的变形。它使用减精度来表示 bin 区间的中心,即它的每一个区间都是用一个更低精度的数来表示,具体来说就是四舍五入啦。下面是一个对 1-100 的数据列建立 bak 索引的输出,其中第一列表示区间的中心,第二三列代表区间最小最大值,第四列代表该区间内数据的个数:
index (equality encoding on reduced precision values) for data.a contains 19 bitvectors for 100 objects 1 1 1 1 2 2 2 1 3 3 3 1 4 4 4 1 5 5 5 1 6 6 6 1 7 7 7 1 8 8 8 1 9 9 9 1 10 10 14 5 20 15 24 10 30 25 34 10 40 35 44 10 50 45 54 10 60 55 65 11 70 66 74 9 80 75 84 10 90 85 94 10 100 95 100 6
4.4 bin->bak2
bak2 (定义于 ibin.h,实现于 idbak2.cpp)是 bak 的变形,也是以减精度来表示区间。但与 bak 不同的是,它将 bak 的每个区间区分为两个区间:小于减精度数的区间,和大于等于减精度数的区间。虽然注释中这样说,但实现时 bak2 是将 bak 的区间分为了三个:小于、等于和大于。下面是一个对 1-100 的数据列建立 bak2 索引的输出,每列的含义与 bak 中示例相同:
index (equality encoding on reduced precision values) for data.a contains 37 bitvectors for 100 objects 1 1 1 1 2 2 2 1 3 3 3 1 4 4 4 1 5 5 5 1 6 6 6 1 7 7 7 1 8 8 8 1 9 9 9 1 10 10 10 1 10 11 14 4 15 15 19 5 20 20 20 1 20 21 24 4 25 25 29 5 30 30 30 1 30 31 34 4 35 35 39 5 40 40 40 1 40 41 44 4 45 45 49 5 50 50 50 1 50 51 54 4 55 55 59 5 60 60 60 1 60 61 65 5 66 66 69 4 70 70 70 1 70 71 74 4 75 75 79 5 80 80 80 1 80 81 84 4 85 85 89 5 90 90 90 1 90 91 94 4 95 95 99 5 100 100 100 1
除了上面几个算法之外,扩展的算法还有 roster 和 keywords,这两种算法比较复杂,这里就不示例讲解了。
五、多层 bitmap 索引算法
有了几个基础的 bitmap 索引算法,我们就可以考虑将这些算法组合成一个层次的结构,构造出多层的 bitmap 索引算法。下面的几个算法,即是由前面的基础 bitmap 索引算法构造出来的二(多)层 bitmap 索引算法。
5.1 bin->ambit
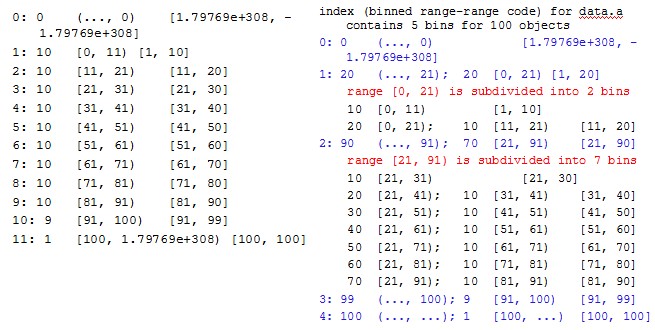
ambit(定义于 ibin.h,实现于 ixambit.cpp)是 multilevel-range based算法,在这个算法中索引分为多层,每层索引都是基于 range 的索引。具体实现时,fastbit 首先构造 bin,然后对桶进行分组(调用 bin::divideBitmaps),然后构造 ambit。分组粒度可以由命令行传入参数 ncoarse=x 和/或 nrefine=n 指定,否则由一简单算法确定,确定分组个数的算法为(第一个桶不参与分组):
ixambit.cpp: 33 // the default number of coarse bins is determined based on a set 34 // of simplified assumptions about expected sizes of range encoded 35 // bitmaps and word size being 32 bits. 36 const uint32_t defaultJ = static_cast37 (nbins < 100 ? sqrt((double)nbins) : 38 0.5*(31.0 + sqrt(31.0*(31 + 4.0*nbins))));
下面看一个实际的例子,左侧是对 1-100 的数据列构造的 bin,右侧是基于该 bin 构造的 ambit:
5.2 bin->pale
pale(定义于 ibin.h,实现于 ixpale.cpp)是 two-level binned equality-range算法,它的索引分为两层,第一层为 binned equality(bin) 索引,第二层为 range 索引。在具体实现时,pale 首先构造 bin,然后对桶进行分组(调用 bin::divideBitmaps),然后构造 pale。与 ambit 相同,分组粒度可以由命令行传入参数 ncoarse=x 和/或 nrefine=n 指定,否则当 bin 桶数大于31时,默认第一层为16个组:
ixpale.cpp:
45 else { // default -- 16 coarse bins
46 if (nbins > 31) {
47 j = 16;
48 }
49 else {
50 j = nbins;
51 }
52 }
下面看一个实际的例子,左侧是对 1-100 的数据列构造的 bin,右侧是基于该 bin 构造的 pale:
5.3 bin->pack
pack(定义于 ibin.h,实现于 ixpack.cpp)是 two-level binned range-equality 算法。它的索引分两层,与 pale 相反,第一层为 range 索引,第二层为 binned equality(bin) 索引。具体实现时,fastbit 首先构造 bin,然后对桶进行分组(调用bin::divideBitmaps),然后构造 pack。分组粒度可以由命令行传入参数 ncoarse=x 和/或 nrefine=n 指定,否则当bin桶数大于63时,默认第一层为31个组:
ixpack.cpp:
44 else { // default -- 31 coarse bins
45 if (nbins > 63) {
46 j = 31;
47 }
48 else {
49 j = nbins;
50 }
51 }
下面看一个实际的例子,左侧是对 1-100 的数据列构造的 bin,右侧是基于该 bin 构造的 pack:
5.4 bin->zone
zone(定义于 ibin.h,实现于 ixzone.cpp)是 two-level binned equality-equality 算法,它的索引分两层,两层均为 binned equality(bin) 索引。它的实现方式也是首先构造 bin,然后对桶进行分组(调用 bin::divideBitmaps),然后构造 zone。其分组粒度可以由命令行传入参数 ncoarse=x 和/或 nrefine=n 指定,否则当bin桶数大于31时,默认第一层为14个组:
ixpack.cpp:
46 else { // default -- 14 coarse bins
47 if (nbins > 31) {
48 j = 14;
49 }
50 else {
51 j = nbins;
52 }
53 }
下面看一个实际的例子,左侧是对 1-100 的数据列构造的 bin,右侧是基于该 bin 构造的 zone:
5.5 bin->fuge
fuge(定义于 ibin.h,实现于 ixfuge.cpp)是 two-level binned interval-equality 算法,fuge 为德语中 interstice 的表述。fuge 的索引分两层,第一层为 interval(mesa) 索引,第二层为 binned equality(bin) 索引,它也是采用首先构造 bin,然后基于 bin 构造 fuge 的方式。其分组粒度由 ncoarse=x 指定,否则默认的分组个数由下面算法确定:
ixfuge.cpp: 887 // default size based on the size of fine level index sf: sf(w-1)/N/sqrt(2) ... 899 if (ncoarse < 5U && offset32.back() > 900 offset32[0]+static_cast(nrows/31)) { 901 ncoarse = sizeof(ibis::bitvector::word_t); ... 913 else { 914 ncoarse = ncmax; 915 } 916 }
下面看一个实际的例子,左侧是对 1-100 的数据列构造的 bin,右侧是基于该 bin 构造的 fuge:
5.6 relic->bylt
bylt(定义于 irelic.h,实现于 ixrelic.cpp)是 two-level unbinned range-equality 算法,bylt 是丹麦语的 pack(binned 版本算法)。bylt 索引分两层,第一层为 range 索引,第二层为 unbinned equality(relic) 索引。在实现时首先构造 relic,然后对桶进行分组(调用bin::divideBitmaps),然后构造 bylt。分组粒度可以由 ncoarse=x 指定,bylt 保证每组中桶数是大致均匀的,否则由下面算法决定分组的个数:
ixbylt.cpp:
182 // default size based on the size of fine level index sf:
183 // (w-1) * sqrt(sf*(sf-N/(w-1))) / (2N)
184 if (ncoarse < 5U && offset64.back() > offset64[0]+(int32_t)(nrows/31U)) {
185 ncoarse = sizeof(ibis::bitvector::word_t);
const int wm1 = ncoarse*8-1;
...
199 ncoarse = ncmax;
200 }
201 }
下面看一个实际的例子,左侧是对 1-100 的数据列构造的 relic,右侧是基于该 relic 构造的 bylt:
5.7 relic->fuzz
fuzz(定义于 irelic.h,实现于 ixfuzz.cpp)是two-level unbinned interval-equality 算法,即 fuge 的 unbinned 版本,名字起源于 fuzzy 聚类/分类。fuzz 索引分两层,第一层为 interval(mesa) 索引,第二层为 unbinned equality(relic) 索引,具体实现时 fastbit 也是采用首先构造 relic,然后构造 fuzz 的方式。其分组粒度可以由 ncoarse=x 指定,否则默认分组个数由下面算法确定:
ixfuzz.cpp:
168 // default size based on the size of fine level index sf: sf(w-1)/N/ sqrt(2)
169 if (ncoarse < 5U && offset64.back() > offset64[0]+nrows/31U) {
170 ncoarse = sizeof(ibis::bitvector::word_t);
...
182 else {
183 ncoarse = ncmax;
184 }
185 }
下面看一个实际的例子,左侧是对 1-100 的数据列构造的 relic,右侧是基于该 relic 构造的 fuzz:
5.8 relic->zona
zona(定义于 irelic.h,实现于 ixzona.cpp)是 two-level unbinned equality-equality 算法,zona 是丹麦语的zone(binned 版本算法),其索引分两层,两层均为 unbinned equality(relic) 索引。首先构造 relic,然后对桶进行分组构造zona,分组个数默认为11个。下面看一个实际的例子,左侧是对 1-100 的数据列构造的 relic,右侧是基于该 relic 构造的 zona:
六、多成分 bitmap 索引
多成分(multi-component)bitmap 索引[3]是使用一组基数将数据值分解成多个部分,分别对每个部分进行 bitmap 索引的方案。原理描述如下:给定 n-1 个基数 { bn-1, bn-2, ..., b1},那么一个值 v 可以通过下式分解为 {vn, vn-1, ..., v1}:
这和数的表示法类似,如果令 bi 都是 10,那么 vi 就是十进制表示法中第 i 位的值(大于等于0,小于10)。更准确的表述可以参考[3]。下面我们来看 fastbit 中的几个实现。
6.1 relic->fade
fade(定义于 irelic.h,实现于 ifade.cpp)是 multicomponent range-encoded 算法,即在每个部分中,是使用的 range 索引。下面来看一个 range-encoded 的例子:
在(b)图中,选择的基数是 9,那么索引就变成了一个单成分的 range 索引算法;在(c)图中,选择的基数是 <3, 3> 这样一个双成分编码,对分解出来的每个成分(大于等于0,小于3)生成 range 索引,就得出了 (c) 图中的结果。
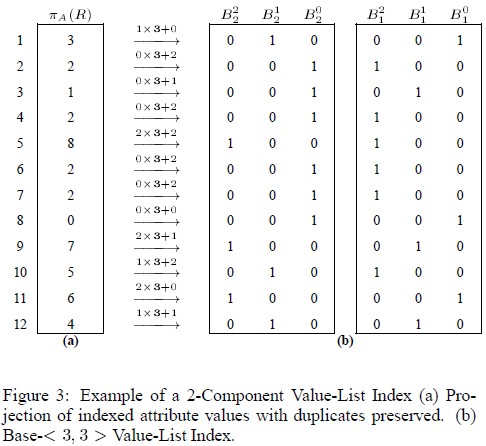
6.2 relic->fade->sapid
sapid(定义于 irelic.h,实现于 isapid.cpp)是 multicomponent equality-encoded 算法,即在每个部分中是使用的 equality(relic) 索引。下面来看一个 equality-encoded 的例子:
在(b)图中,选择的基数是 <3, 4> 这样一个双成分编码,对分解出来的每个成分生成 relic 索引,就得到了 (b) 图中的索引结果。
除了这两个索引算法之外,还有 sbiad(multicomponent interval-encoded),egale(multicomponent equality code on bins), entre(multicomponent interval code on bins), moins(multicomponent range code on bins)这几个索引算法。从括号中我们可以大致猜出这些索引的实现方式,但是由于我们现在没有一个很好的示例展现方式,用实际用例来展现这些索引算法的效果将会留给以后的文章进行。
七、总结
这篇文章基于 fastbit 软件包,加以实际的用例对常用的 bitmap 索引算法进行了一个较为系统的介绍。不过生成 bitmap 索引仅仅是第一步,bitmap 索引在存储时会有很大的开销,在不损害(较少损害)查询效率的情况下,对 bitmap 索引进行有效的压缩是一个非常有挑战性的课题。除了 bitmap 索引的生成和存储之外,在不同类型的 bitmap 索引上实现高效的各种类型的查询,也是一个值得进一步探讨的问题。我们很高兴地看到 fastbit 软件包实现了很多这些相关领域的算法,为我们提供了非常宝贵的资料。
参考文献
[1] C-Y. Chan and Y. E. Ioannidis, An efficient bitmap encoding scheme for selection queries, in Proceedings of the ACM international conference on Management of data (SIGMOD), 1999.
[2] P. O’Neil and DalIan Quass, Improved Query Performance with Variant Indexes, in Proceedings of the ACM international conference on Management of data (SIGMOD), 1997.
[3] C-Y. Chan and Y. E. Ioannidis, Bitmap Index Design and Evaluation, in Proceedings of the ACM international conference on Management of data (SIGMOD), 1998.