最近人人都在聊 ChatGPT,这里聊点儿更底层的技术细节。上周 OpenAI 发布了 GPT-4,里面有一张图引起了我的兴趣。在 OpenAI 内部的 Codebase 上,他们准确预测了 next word prediction 误差随着计算规模增加的下降曲线。让我感兴趣的不是这个曲线,而是这个曲线纵轴使用的指标:Bits Per Word (BPW)。
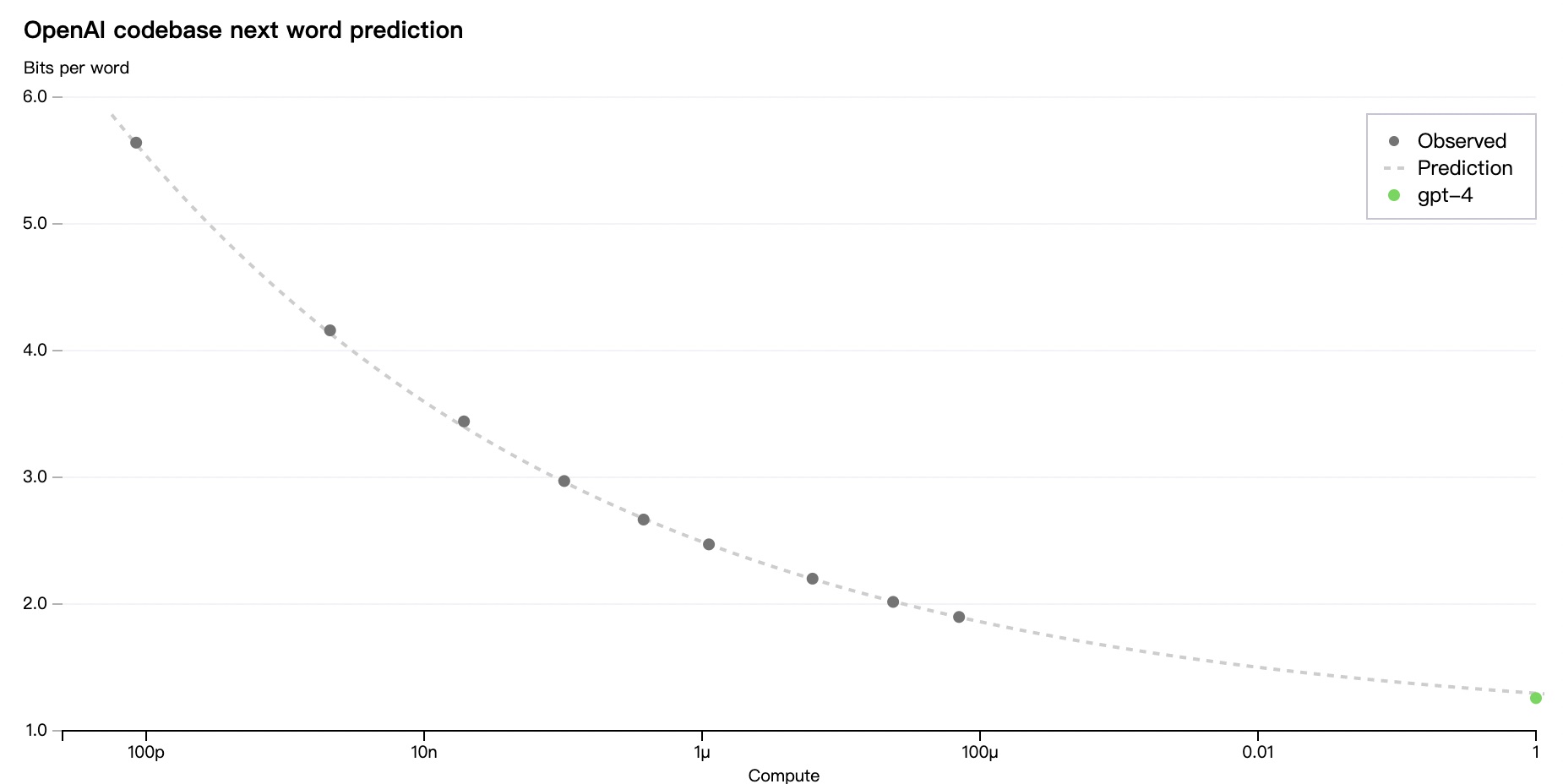
乍一看我以为这是信息论里的概念,Bits Per Word 可能是指在某种语言里表达一个词所需要的最小位数,比如用于压缩时,这意味着压缩比的理论上限。但仔细看下指标接近 1.2 BPW,虽说英文字母的 Bits Per Character (BPC) 大约也在 1.2 左右,我不太相信单词的 BPW 能降到 1.2 这个规模。
后来才了解到,Bits Per Character (BPC) / Bits Per Word (BPW) 是 NLP 任务中对语言模型的评估指标之一。这些评估指标的详细解释可以先阅读这篇文章《Evaluation Metrics for Language Modeling》,但是我感觉这篇文章的说明在理论和应用之间跳过了一些环节,下面我以我的理解补全一下这些环节。推测的内容以黑字标出,如有谬误,欢迎指正。
原始 BPW 定义
The entropy is a statistical parameter which measures, in a certain sense, how much information is produced on the average for each letter of a text in the language. If the language is translated into binary digits (0 or 1) in the most efficient way, the entropy \(H\) is the average number of binary digits required per letter of the original language.
以上,是香农在《Prediction and Entropy of Printed English》一文中对语言的熵的定义。可以看到,语言的熵 \(H\) 其实就是 BPC (Bits Per Character) 的均值。但我们一般不会报告某个字符有几个 bits,因而通常所说的 BPC,就是整个语言(数据集)的平均 BPC,所以可以理解为语言的熵 \(H\) 就是 BPC。
但是在原始论文中,香农是用字符来建模的语言的熵,当用单词来建模语言时,语言的熵 \(H\) 就是 BPW (Bits Per Word)。
用 BPW 表示交叉熵
对于生成式语言模型来说,它的目标就是从样本中学习到一个分布 \(Q\),使这个分布尽量接近语言的经验分布 \(P\)。交叉熵 \(H(P, Q)\) 经常被用来衡量这种接近程度,
\[H(P, Q) = H(P) + D_{KL}(P \Vert Q) \]
根据 《Evaluation》 一文,交叉熵的两个因子用信息论的角度来理解:
- \(H(P)\): 就是 \(P\) 的熵,即使用为分布 \(P\) 优化的编码器编码 \(P\) 中所有可能出现的字符的平均位数;
- \(D_{KL}(P \Vert Q)\): 使用为分布 \(Q\) 优化的编码器编码 \(P\) 中所有可能出现的字符,所需要的平均额外位数;
与原始 BPC/BPW 的定义相同,如果用 \(BPC/BPW(P, Q)\) 表示交叉熵 \(H(P, Q)\),那么它意思应该是使用为分布 \(Q\) 优化的编码器编码 \(P\) 中所有可能出现的字符/单词所需要的平均位数。
上面这点理解,与知乎上一篇文章《一文搞懂Language Modeling三大评估标准》存在 diff(飘红部分):
也就是说BPC/BPW是cross-entropy对句子长度的平均,我们可以很容易地得出它的信息论含义:
基于预测的Q序列来编码P序列所需要的额外bit数在句子长度上的平均,也就是平均每一个字母/单词需要额外的bit数。
下面这一节,可能能解释 diff 的由来。
用 BPW 表示损失指标
但是在评估一个语言模型时,我们并不是评估模型输出的整个分布,而是评估模型的输出跟实际样本的不同。拿 GPT-2 模型来说,它是拿模型输出的预测下一个 Token 的 logits 与 label (样本中真实的下一个 Token)计算交叉熵:
The output from the decoder is passed to a language modeling head, which performs a linear transformation to convert the hidden states into logits. The label is the next token in the sequence, which are created by shifting the logits to the right by one. The cross-entropy loss is calculated between the shifted logits and the labels to output the next most likely token.
- logits 是一个 \(Q(x)\) 的向量,表示下一个 Token 是 \(x\) 的概率;
- label 表示样本中下一个 Token 是什么,它是一个 \(P(x)\) 的向量,但只有 x = 下一个 Token 时为 1,其它位置为 0,那么:
\[H(P) = -\sum_{x}P(x)\log{P(x)} = 0\]
从信息论也好理解,在计算损失时样本 \(P\) 是一个确定性分布,确定性分布的熵应该为 0。那么在计算交叉熵损失的场景下:
\[H(P, Q) = H(P) + D_{KL}(P \Vert Q) = 0 + D_{KL}(P \Vert Q)\]
可以看到,这时候交叉熵等于相关熵,那么 \(BPC/BPW(P, Q)\) 也就是 \(D_{KL}(P \Vert Q)\),或者更精确地说,是在数据集样本上平均的 \(D_{KL}(P \Vert Q)\)。那么在评估一个语言模型的场景下,把 BPC/BPW 损失指标的信息学含义解释成:“使用为分布 \(Q\) 优化的编码器编码 \(P\) 中所有可能出现的字符/单词所需要的平均额外位数”,也是合理的了。
GPT-4 的 BPW 指标
从 GPT-4 给出的指标来看,它的 BPW 指标只有 1.26 左右。除了信息论编码的概念,这代表什么意思呢?
这里我引入《Evaluation》 一文中提到的另一个指标 Perplexity (PPL) 困惑度和一个有趣的比喻。考虑到:
\[PPL(P, Q) = 2^{H(P, Q)} = 2^{BPW(P, Q)} = 2^{1.26} \approx 2.4\]
那么 GPT-4 语言模型的效果相当于:在给定的数据集上,提供一个样本的前缀串后,GPT-4 会制作一个包含下一个 Token 的 2.4 面的新骰子,然后掷骰子来预测下一个 Token 是什么。